Building Correlations Between Filters in Convolutional Neural Networks
Hanli Wang1, Peiqiu Chen1, Sam Kwong2
This project provides the implementation for the method called correlative filters (CF) on the caffe framework. It’s currently merged in the up-to-date version of caffe published on 2016.12.14.
Generally speaking, CF introduces a series of revised 2D convolutional layers , in which filters are initiated and trained jointly in accordance with predefined correlation (correlation, denotes a certain kind of linear transformation here). As compared with the conventional CNN, CFs are efficient to work cooperatively and finally make a more generalized optical system.
The primitive version of CF, including the opposite CF and the translational CF, has been published on the conference SMC 2015. The revised version has been accepted by the journal of IEEE Transcation on Cybernetics, in which SCF (Static Correlative Filters) and PCF (Parametric Correlative Filters) are introduced.
Introducing Correlative Filters
In this part, we mainly talk about the motivation and workflow of the proposed CF method.
Deep learning has swept across almost every field of machine learning like a hurricane. To our knowledge, deep neural networks are mostly implemented in an end-to-end fashion, which leads to a trainable feature representation for the given training data. Hence, using the DNN model, few task specific knowledge is needed to build an acceptable recognition system. Nevertheless, the outstanding performance achieved by CNN as compared with other kinds of deep neural networks partly depends on CNN’s special structure of connections in small neighborhood, which is a kind of particular priori knowledge that guides each unit to just focus on its presupposed patch of view. Based on this thought, it is reasonable to design a more optimized architecture which brings in more priori information that contributes to optical representation while retaining the flexibility and adaptability of trainable feature extractors.
Motivation
Story behind correlative filters.
Collaboration in Biological Visual Systems
In the very early stage of primate subcortical vision systems, there exist cells with center-surround receptive fields which come into two types: one is sensitive to bright spot on dark background whereas the other focuses on the inverse pattern. They are believed to help extract visual patterns under variant luminance, as shown in Fig. 1.

Figure 1 Center-surround receptive fields sensitive to opposite patterns.
Collaboration in CNN
As multiple filters have always been recognized as receptive fields of CNN, we visualize the filter banks of a normally trained network to examine whether the similar phenomenon occurs, as illustrated in Fig. 2.
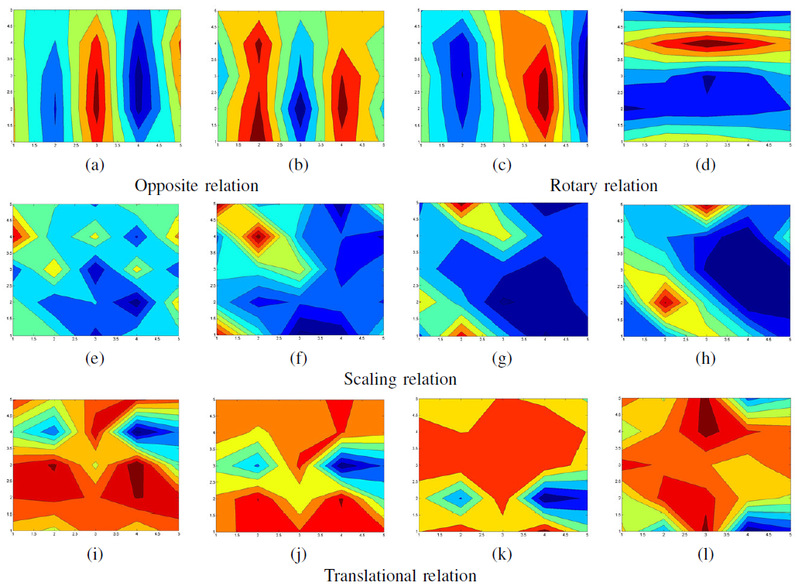
Figure 2 Illustration of the observed relations between normally trained filters.
We found four kinds of relationship. Note that all the weights of filters are randomly initialized with Gaussian distribution and trained freely with the method of stochastic gradient descent, hence these observed relations indicate the cooperation of correlated filters benefits for extracting visual features. According to the observation above, we came up with the idea to realize those relationship before training.
Work Flow
Brief introduction of SCF and PCF, for more details, please refer to our paper on TC.
Static Correlative Filters
To simulate the collaboration discovered, we designed four kinds of static correlative filters, in which each pair of master filter and dependent filter are predefined to have a static relationship, as explained in Fig. 3.
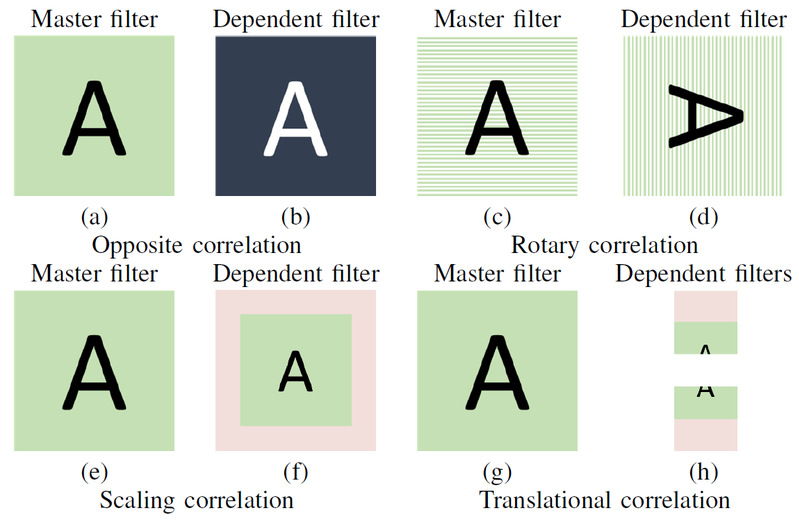
Figure 3 Illustration of the proposed four kinds of SCFs.
The forward pass of SCF is the same as the normal convolutional layers and the flow chart of back-propagation is refined as follows.
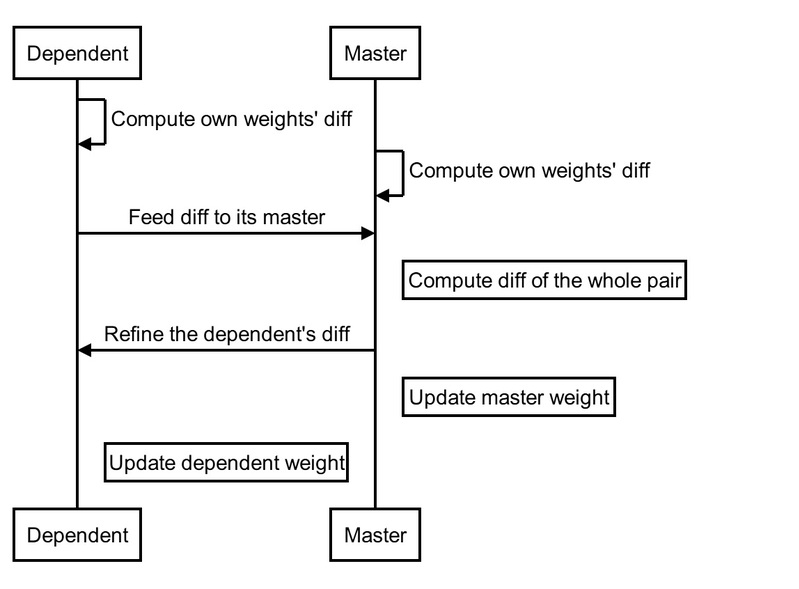
Figure 4 Back-propagation of SCFs.
Parametric Correlative Filters
Besides the proposed SCFs, there might exist other linear correlations that have not been observed intuitively. As an extension to SCF, we came up with the idea to construct trainable correlations by making the correlation matrix learnable during the network training, which leads to the proposed parametric correlative filter (PCF). An illustration about how to train the proposed PCF is presented in the figure below.
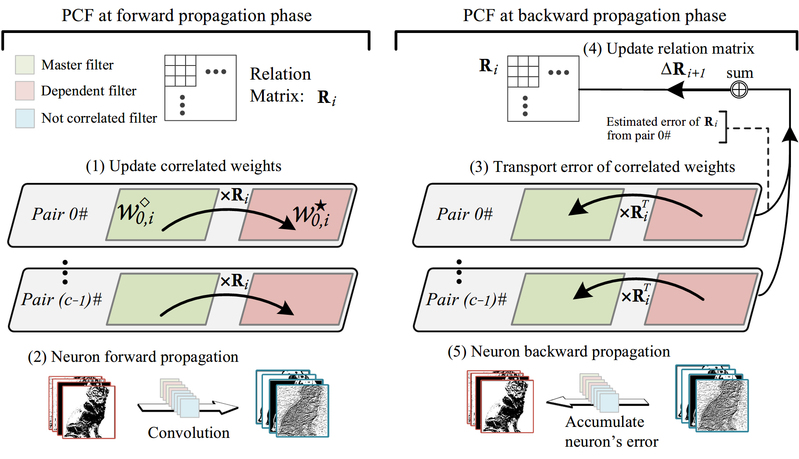
Figure 5 Illustration of training parametric correlative filters.
Instructions for use
Manual of where and how to use convolutional layers applied with CF.
In our implementation, the 2D convolutional layers applied with different kinds of CF are realized as the separated types of layers.
ORfusionConvolutionLayer
This layer supports the opposite CF and the rotary CF. This layer has better performance when placed near the input data layer.
A sample for the ORfusionConvolutionLayer is shown below.
layer {
name: "conv1_0"
type: "ORfusionConvolution"
bottom: "data"
top: "conv1_0"
param {
lr_mult: 1
decay_mult: 1
}
param {
lr_mult: 2
decay_mult: 0
}
convolution_param {
num_output:96
pad: 1
kernel_size: 3
stride: 1
weight_filler {
type: "gaussian"
std: 0.08
}
bias_filler {
type: "constant"
}
}
correlative_filters_param {
opposite_num: 25
rotate_num: 12
}
}
Compared with the normal covolutional layer, we only made two modifications:
The field of type is changed as ORfusionConvolution.
We add the parameter field of correlative_filters_param in which the number of opposite CF and rotary CF in each input channel is listed.
In the sample code, this layer takes the data (three channels for CIFAR-10) as the input layer, so that 75 pairs of opposite and 36 pairs of rotary correlations are defined. If you want to use only opposite/rotary CF in this layer, just set the rotate/opposite_num as zero.
ScaleConvolutionLayer
This layer supports the scaling CF.
Just like the sample code in ORfusionConvolutionLayer, we only need to edit the type and correlative_filters_param.
layer {
name: "conv2_0"
type: "ScaleConvolution"
bottom: "pool1"
top: "conv2_0"
convolution_param{
num_output:160
...
}
correlative_filters_param{
scale_num:5
scale_trans_source:"scale_transform.rawmatrix"
}
}
As shown in the sample code, the scaling CF uses the parameter named scale_num to notify that each output feature map has 5 pairs of scaling CF filters, so that 800 pairs of scaling CF are defined in the sample code. scale_trans_source denotes the file that saves the transform matrix of scaling CF.
TranslationConvolutionLayer
This layer supports the translational CF.
Similarly, to activate the translational CF, the modifications of type and correlative_filters_param are required.
layer {
name: "conv3_0"
type: "TranslationConvolution"
bottom: "pool2"
top: "conv3_0"
convolution_param{
num_output:256
...
}
correlative_filters_param{
translation_horizon_num: 10
translation_vertical_num: 10
}
}
Parameter translation_horizon_num means the number of groups where the horizontal translation is applied.
Parameter translation_vertical_num means the number of groups where the vertical translation is applied.
In the given sample code, both horizontal translation and vertical translation have 2560 groups of translational CF.
ParamCfConvolutionLayer
This layer supports the parametric CF.
The sample code for PCF is shown below.
layer {
name: "conv2_0"
type: "ParamCfConvolution"
bottom: "pool1"
top: "conv2_0"
convolution_param{
num_output:160
...
}
correlative_filters_param{
param_cf_num: 10
}
}
In the given sample code, 1600 pairs of parametric CF are defined.
Download & Citation
Download the source code: ![]() CF_Caffe.zip
CF_Caffe.zip
Please cite our paper in your publications if this project helps your research:
@article{wang2017cfcnn,
title={Building Correlations Between Filters in Convolutional Neural Networks},
author={Wang, Hanli and Chen, Peiqiu and Kwong, Sam},
journal={IEEE Transactions on Cybernetics},volume={47},number={10), pages={3218-3229},
month={Oct.}, year={2017}, doi={10.1109/TCYB.2016.2633552}
}
Feedback & Bug Report
Email: hanliwang@tongji.edu.cn, 14payenjoe@tongji.edu.cn
H. Wang and P. Chen are with the Department of Computer Science & Technology and Key Laboratory of Embedded System and Service Computing, Ministry of Education, Tongji University, Shanghai 200092, P. R. China (e-mail: hanliwang@tongji.edu.cn, 14payenjoe@tongji.edu.cn). ↩
S. Kwong is with the Department of Computer Science, City University of Hong Kong, Hong Kong, P. R. China (e-mail: cssamk@cityu.edu.hk). ↩
